Editor’s Note: Differentiation is a challenge for all of us. I invited Juan Gomez to share his ideas on how to apply it in math class, and am adding it to The Best Resources On Differentiating Instruction. You can see all my resources on the topic here.
In his 19 years in education, Juan Gomez has served as Dean of Students, Athletic Director, Induction Mentor, Instructional Coach, coached a variety of sports: all while teaching at least four sections of a variety of math classes. His current interest is differentiation in the math classroom.
Differentiation. Most years I teach about 120 students- on the lower end of things for a high school math teacher. This is due, in part, to my work as an instructional coach. Instructional coaching takes me out of my own classroom and into those of my peers- a very insightful process. As a coach, a frequent request in our learning cycles is, “How do I differentiate instruction?”. During the coaching pre-planning meeting we narrow down the focus of what differentiation looks like for that teacher. Inevitably, we end up at a place where the teacher envisions differentiation as a different lesson scripted for each child. In math, differentiation often takes on a few different looks: creating an “easy”, “medium”, “challenge” set of problems, splitting up your students into remediation groups, or assigning students that fall behind an extra class period where they can get help in order to get back on grade level. In a few cases, we also consider differentiation as helping advanced learners move forward faster than their peers. Although differentiation for advanced learners can also have many forms, in my experience it frequently takes the shape of grouping high achieving students into sequence of courses where all students within them are homogeneously high achieving or assigned optional problems that are more intricate versions of those they have already seen.
The struggle with any of these ways to differentiate is that they require a lot of work from the teacher or can only happen with institutional change.
Recently, I saw Larry Ferlazzo’s video on differentiating instruction. In it he proposes that differentiating instruction is not “ a pre-planned list of strategies, but rather a way of thinking. Often times it is making decisions in the moment.” This definition of differentiation struck a chord with me- to the point where I decided to share some of the ways I differentiate in my classroom at the California Math Council’s North Conference at Asilomar. In the video, Larry mentions that “thinking flexibly in the moment” often leads to differentiating process, content, or product. In the paragraphs below I’ll share some of the ways I think differently in the moment with my students. If you’re interested in the full slide deck that I shared at CMC-North you can click here.
Differentiate Process:
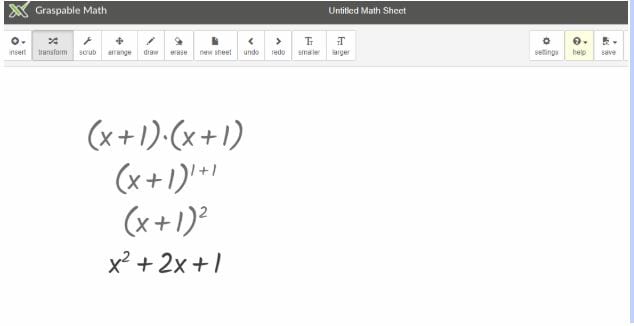
In a math class, we constantly strive to move a student’s mathematical thinking forward. This is inevitably hampered by any gaps in content. As an example, I shared a way I adapt the process for students in my Integrated Math 3 class so they can understand the patterns behind Binomial Expansion, even though they may struggle with algebra. When I see students struggle with algebra, I direct them to Graspable Math. This freely available tool helps students work with abstract expressions-but- it will only execute the command if it is mathematically valid. For example, if a students tries to “distribute an exponent” Graspable Math will not follow through, leaving the original content on the workspace. My students are able to work through and see patterns in a binomial expansion, while fine tuning their understanding of what correct algebra should look like. Below is an example of what the Graspable Math workspace looks like.
Other times I have used Desmos as a tool to allow students creative freedom in expressing understanding of graphing functions. A popular form of this is to have students create a coloring book made from pictures made using functions graphed in Desmos. Students are given the parameters within which they should work. They then have creative freedom to make any picture they wish. Below is a Halloween-themed spider created by students in Luke Walsh’s classroom. In my experience, students are equally challenged and delighted by the work. While most of my students use linear, quadratic, rational, and exponential functions to create their coloring book page, typically I will have one or two students who are up for the challenge of incorporating domain and range restrictions or sinusoidal functions.
Differentiate the Product:
As a Desmos Fellow, I frequently use many of freely available activities to engage students in thinking about math before we do it. If you have never used the Desmos Activity Builder platform, you are in for a treat! As a teacher, you find a prebuilt activity to assign to students and deploy it by creating a class code. You are then able to pace students through the activity using the pacing feature as well as take snapshots of student work to create class conversations. To find out what this looks like from a student’s point of view, you can try the “Point Collector” activity by going to student.desmos.com and using the class code “Q2JTFH”. You will be as surprised as I am by the variety of mathematically correct answers your students will provide. While I have many different ways to differentiate student product, Desmos is the most entertaining option for both the students and myself.
Differentiate the Content
As a veteran teacher in his first year teaching Advanced Placement Statistics, I am aware that I am teaching to the AP exam. However, I also know I have a choice in the context students use to learn statistics. One way I have chosen to differentiate the content is by using data students have gathered. This Halloween we used John Orr’s Pumpkin Time Bomb (link here) to both gather data and compare it to students from other states who had also completed the activity. Gathering data and combining it with other students allowed us to have a data set that we “owned” and have come back to several times during the semester. Students were very proud of “their” pumpkin – many naming it and talking about its resilience to the rubber bands that would inevitably cause it to collapse.
In my work as a coach, I will continue to encourage teachers to “think flexibly in the moment” and rethink the restraints of what math class should look like. Our students can’t wait.





Recent Comments